VAE

• VAE는 직접적으로 ELBO를 maximize 한다.
• variational : 확률 분포를 추론한다는 뜻. VAE는 $\phi$ 를 추론하기 때문에 Variational.
• AutoEncoder : bottleneck을 거쳐서 원본데이터를 추론함

• $q_\phi(z|x) = encoder, p_\theta(x|z) = decoder$
• prior matching term = 학습중인 $q_\phi(z|x)$ 가 우리가 prior로 믿고있던 $p(z)$ 와 얼마나 비슷한가?
• reconstruction term = variational distribution $q_\phi(z|x)$ 에서 x를 얼마나 잘 재현하나

• 결국 VAE의 핵심은 $\phi$ 와 $\theta$ 에 의해 얼마나 ELBO를 최적화했냐의 문제임
• 일반적으로 encoder는 대각공분산을 가진 다변수 정규분포 $q_\phi(z|x) = \mathcal{N}(z;\mu_\phi(x), \sigma^2_\phi(x)I)$ 로 설정됨. 즉, x에 대한 z의 예측값을 다변수정규분포라고 가정
• 일반적으로 prior는 표준정규분포 $p(z) = \mathcal{N}(z;0,I)$ 로 설정됨. 즉, z의 사전분포의 진실은 표준정규분포라고 가정
• 왜냐??
  1. 이렇게 했을 때 ELBO의 $D_{KL}$이 analytically 계산될 수 있기 때문 (iteration을 통해 미분값을 구해서 개선하는 방식. ex : Neuton’s method)
  2. reconstruction term 또한 Monte Carlo estimate 를 활용해서 근사될 수 있기 때문
• 최종 목적함수는 다음과 같다

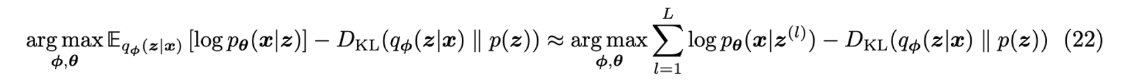
• latents $\{z^{(l)}\}^L_{l=1}$ 는 $q_\phi(z|x)$ 에서 샘플링됨. 근데 이때 stochastically sampled 되기 때문에 미분불가능함. → 이건 reparameterization trick을 활용해서 해결 가능하다.
  • reparameterization trick : 확률변수를 noise variable의 deterministic function 으로 재구성하는 것이다. 예를 들어, $x\sim\mathcal{N}(x;\mu,\sigma^2)$ 에서 샘플링하는 걸 $x=\mu+\sigma\epsilon~~ (\epsilon\sim\mathcal{N}(0,I))$ 으로 변경하는거임. 따라서 VAE에서는 reparameteraization trick에 의해 $z=\mu_\phi(x)+\sigma_\phi(x)\odot\epsilon$ 이 되고, $\phi$ 에 대해 미분을 할 수 있게 된다.
• 이제, 학습이 끝나면 latent space $p(z)$ 에서 z를 샘플링한다음에 generation 해버리면 된다. 의도를 집어넣으려면 semantically meaningful latent space를 학습해야 한다.